Combining Functions & Purrr for simulations
A short guide to doing simulations with purrr
A simple example
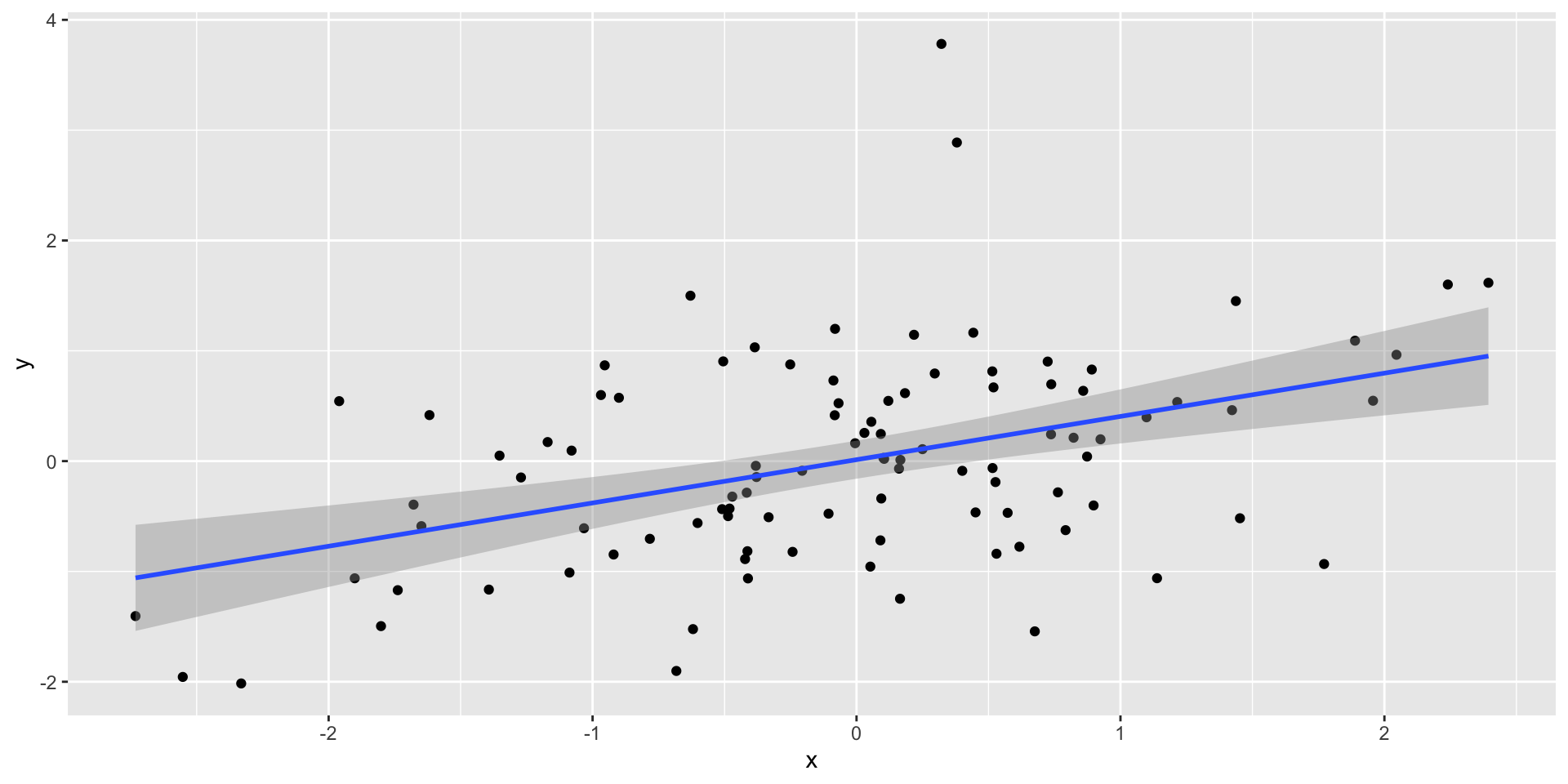
Let’s say we want to calculate the power to detect a correlation of .31
enter purrr
# Define a function that generates a random dataset
generate_data <- function(x){
# adding the x as an argument is a bit of a hack because we don't need it
# there's an easier way to do this in R using the replicate function
measure_1 <- rnorm(100)
measure_2 <- measure_1 * 0.3 + rnorm(100)
result <- data.frame(measure_1, measure_2)
}simulations_data <- tibble(simulation_id = c(1:1000)) %>%
mutate(sim_dat = map(simulation_id, generate_data),
model = map(sim_dat, \(x) {lm(measure_2 ~ measure_1, data = x)}),
tidy_model = map(model, broom::tidy),
p_value_measure_2 = map_dbl(tidy_model, \(x) x %>%
filter(term == "measure_1") %>%
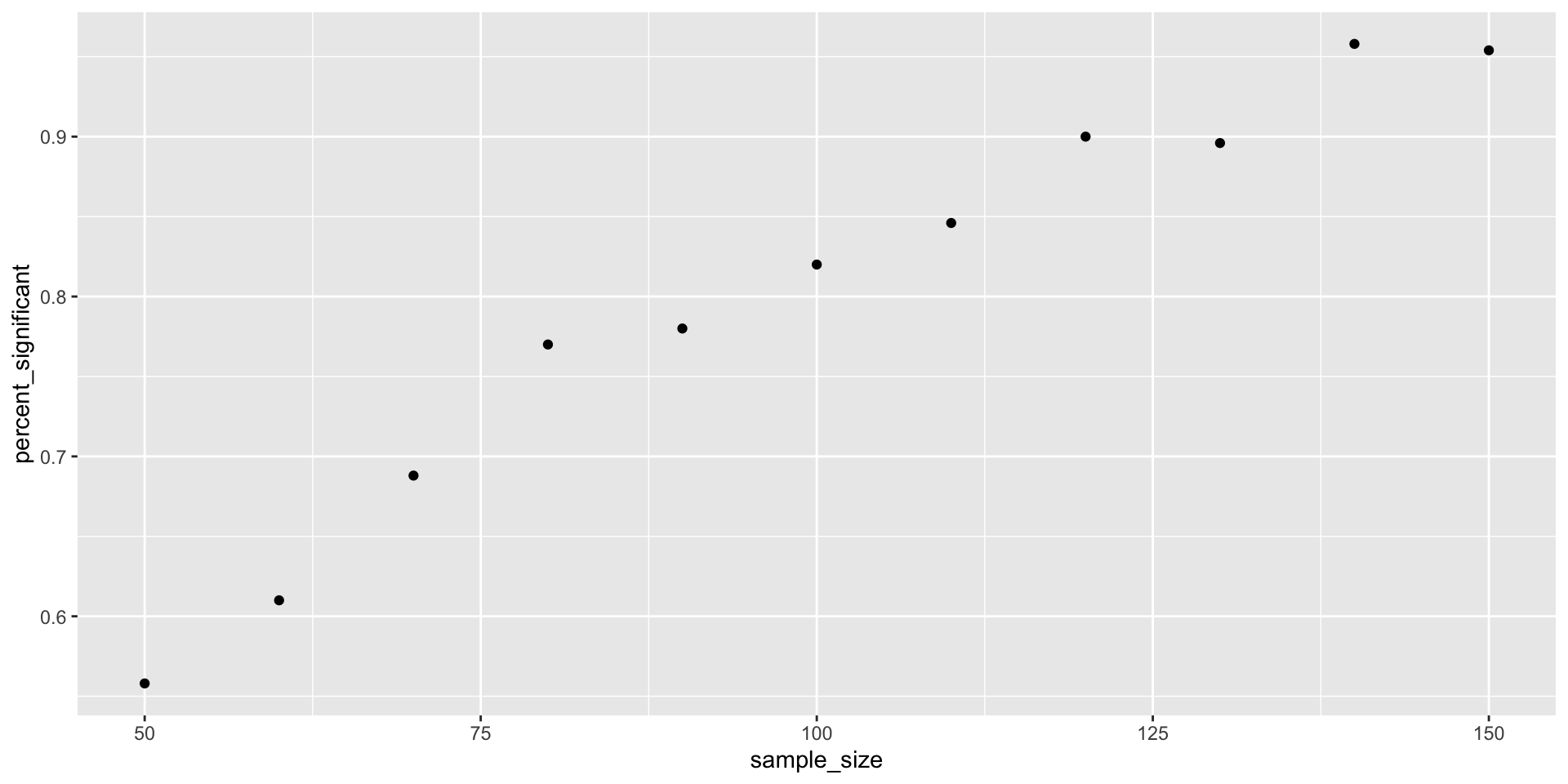
pull(p.value)))This is nice, but only for a fixed sample size…
Let’s try and make it better :)
sim_outcome %>%
unnest(tidy_model) %>%
filter(term == "measure_1") %>%
group_by(sample_size) %>%
summarise(across(c(estimate, std.error), c("mean" = mean), .names = "{.fn}_{.col}")) %>%
ggplot(aes(sample_size, mean_estimate, ymin = mean_estimate - mean_std.error, ymax = mean_estimate + mean_std.error)) +
geom_pointrange() +
expand_limits(y = c(0, 0.35))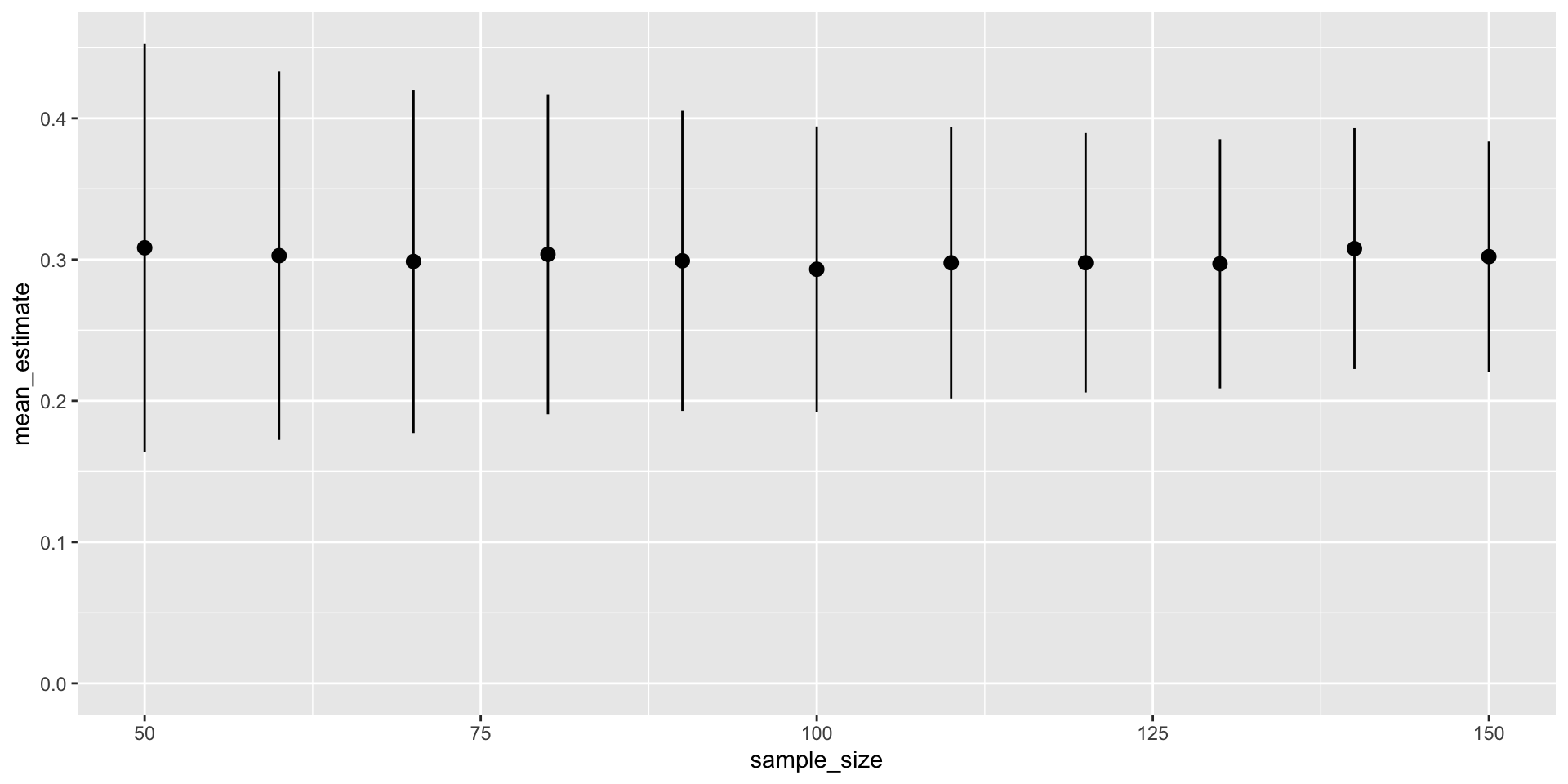
Practice: Do the same for a t-test
Bonus: what about different effect sizes?
Resources
- this blog by Solomun Kurz
- the simglm package that does a lot of the work for you.
- this blogpost by Lisa DeBruine also covers parallelisation